图作为一种重要的数据结构,广泛应用于通信线路的规划与管理中。图的遍历算法包括深度优先搜索(DFS)和广度优先搜索(BFS),而最小生成树和最短路径算法则用于优化通信网络结构和资源分配。
图的遍历:深度优先搜索(DFS)
深度优先搜索是一种沿着图的分支深入探索的遍历方法。在通信线路中,DFS可用于检测网络的连通性或查找特定路径。例如,假设通信网络由多个节点(如基站)和边(如光纤线路)组成,DFS可以从起点出发,优先访问一条路径直到尽头,再回溯探索其他分支。这种方法有助于识别孤立的节点或检查网络是否存在环路,从而优化维护策略。
图的遍历:广度优先搜索(BFS)
广度优先搜索是一种逐层扩展的遍历方式,从起点开始先访问所有相邻节点,再逐步向外扩展。在通信线路中,BFS常用于计算最短路径或广播信息。例如,在部署新通信服务时,BFS可以帮助确定从中心节点到所有其他节点的最短跳数,确保信号传输效率。与DFS相比,BFS更适合处理层次化网络结构,如城市通信塔的覆盖范围分析。
最小生成树(MST)
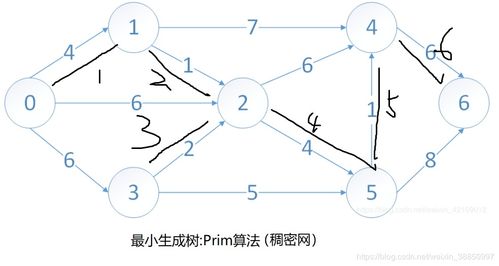
最小生成树算法(如Prim或Kruskal算法)用于在加权图中找到连接所有节点的最小成本子图。在通信线路中,MST可优化基础设施建设成本。例如,规划一个覆盖多个城市的通信网络时,使用MST可以选择总长度最短的光纤线路,避免冗余连接,从而节省材料和维护费用。Kruskal算法通过按权重排序边并避免环路来构建树,而Prim算法则从节点出发逐步扩展,两者都适用于不同规模的通信网络设计。
最短路径算法
最短路径算法(如Dijkstra或Bellman-Ford算法)用于找到图中两点之间的最短路径,考虑边权重(如距离或延迟)。在通信线路中,这直接关系到数据传输效率。例如,互联网路由协议使用最短路径算法来选择数据包的最佳路径,减少延迟并提高可靠性。Dijkstra算法适用于非负权重的网络,而Bellman-Ford算法可处理负权重情况,两者在动态通信环境中至关重要。
综合应用与实例
在实际通信线路管理中,这些算法常结合使用。以5G网络部署为例:DFS和BFS可用于网络拓扑发现和故障诊断;MST帮助设计经济高效的骨干网;最短路径算法则优化数据路由。通过整合这些方法,通信运营商可以提升网络性能、降低成本,并确保服务可靠性。
图的遍历、最小生成树和最短路径算法是通信线路规划与优化的核心技术。掌握这些工具,不仅能提高网络效率,还能应对日益复杂的通信需求。